Solving Ramanujan's Puzzling Problem

Consider a sequence of functions as follows:-

$ f_1 (x) = \sqrt {1+\sqrt {x} } $
$ f_2 (x) = \sqrt{1+ \sqrt {1+2 \sqrt {x} } } $

$ f_3 (x) = \sqrt {1+ \sqrt {1+2 \sqrt {1+3 \sqrt {x} } } } $

......and so on to

$ f_n (x) = \sqrt {1+\sqrt{1+2 \sqrt {1+3 \sqrt {\ldots \sqrt {1+n \sqrt {x} } } } } } $

Evaluate this function as n tends to infinity.

Or logically:

Find

$ \displaystyle{\lim_{n \to \infty}} f_n (x) $ .

Ramanujan discovered

$$ x+n+a=\sqrt{ax + (n+a)^2 +x \sqrt{a(x+n)+(n+a)^2 +(x+n) \sqrt{\ldots}}} $$

which gives the special cases

$$ x+1=\sqrt{1+x \sqrt{1 + (x+1) \sqrt{1 + (x+2) \sqrt{1 + (x+2) \sqrt{\ldots}}}}}$$

for x=2 , n=1 and a=0

$$3= \sqrt{1+2 \sqrt{1+3 \sqrt{1+ 4 \sqrt{1+\cdots}}}}$$

Comparing these two expressions & assuming

=$ X $ , we can write the problem as:

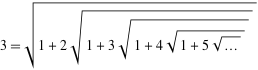
$ \displaystyle {\lim_{n \to \infty}} f_n (x) $

= $ \sqrt {1+X} $

= $ \sqrt {1+3} $

=$ \sqrt {4} $

=$ 2 $

For further info please refer the comments below. There is also a supportive article on Ramanujan Nested Radicals on this blog.