Solving Ramanujan’s Puzzling Problem
Consider a sequence of functions as follows:-
$ f_1 (x) = \sqrt {1+\sqrt {x} } $
$ f_2 (x) = \sqrt{1+ \sqrt {1+2 \sqrt {x} } } $
$ f_3 (x) = \sqrt {1+ \sqrt {1+2 \sqrt {1+3 \sqrt {x} } } } $
……and so on to
$ f_n (x) = \sqrt {1+\sqrt{1+2 \sqrt {1+3 \sqrt {\ldots \sqrt {1+n \sqrt {x} } } } } } $
Evaluate this function as n tends to infinity.
Or logically:
Find
$ \displaystyle{\lim_{n \to \infty}} f_n (x) $ .
Solution
Ramanujan discovered
$$ x+n+a=\sqrt{ax + (n+a)^2 +x \sqrt{a(x+n)+(n+a)^2 +(x+n) \sqrt{\ldots}}} $$
which gives the special cases
$$ x+1=\sqrt{1+x \sqrt{1 + (x+1) \sqrt{1 + (x+2) \sqrt{1 + (x+2) \sqrt{\ldots}}}}}$$
for x=2 , n=1 and a=0
$$3= \sqrt{1+2 \sqrt{1+3 \sqrt{1+ 4 \sqrt{1+\cdots}}}}$$
Comparing these two expressions & assuming
=$ X $ , we can write the problem as:
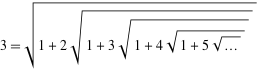
$ \displaystyle {\lim_{n \to \infty}} f_n (x) $
= $ \sqrt {1+X} $
= $ \sqrt {1+3} $
=$ \sqrt {4} $
=$ 2 $
–
For further info please refer the comments below. There is also a supportive article on Ramanujan Nested Radicals on this blog.
I’m not entirely sure, but using C++ (with n = 1,000,000) I numerically evaluated it to the function f(x) = 2. But as I said, not quite sure!
I’m not entirely sure, but using C++ (with n = 1,000,000) I numerically evaluated it to the function f(x) = 2. But as I said, not quite sure!
You’re right..! After using google, I got this Link , which was also saying the same. But I wasn’t satisfied.
Answer is 3 according to formulation 27 at http://mathworld.wolfram.com/NestedRadical.html .
Answer is 3 according to formulation 27 at http://mathworld.wolfram.com/NestedRadical.html .
There are two slightly different versions of this nested radical, so you need to be careful.
The version posed by Ramanujan was
sqrt(1 + 2*sqrt(1 + 3*sqrt(1 + 4*sqrt(1 + … = 3
Your version is almost the same:
sqrt(1 + 1*sqrt(1 + 2*sqrt(1 + 3*sqrt(1 + … = sqrt(1 + 3) = 2.
There are two slightly different versions of this nested radical, so you need to be careful.
The version posed by Ramanujan was
sqrt(1 + 2*sqrt(1 + 3*sqrt(1 + 4*sqrt(1 + … = 3
Your version is almost the same:
sqrt(1 + 1*sqrt(1 + 2*sqrt(1 + 3*sqrt(1 + … = sqrt(1 + 3) = 2.
Hi there,
Just a small typo — I think you meant to write the limit as n tends to infinity. On all of the limits you wrote in that article, you unfortunately said that x goes to infinity.
x_x
x_x Corrected Now. Thanks.
Hi there,
Just a small typo — I think you meant to write the limit as n tends to infinity. On all of the limits you wrote in that article, you unfortunately said that x goes to infinity.
x_x
x_x Corrected Now. Thanks.
wow – wouldnt have a clue where to start!
wow – wouldnt have a clue where to start!
I think you might be one of the best bloggers in India today. We are having a TEDx conference, and it would be great to have you as a Speaker. I am sure you can come up with a very interesting talk. Let me know however I can contact you.
I think you might be one of the best bloggers in India today. We are having a TEDx conference, and it would be great to have you as a Speaker. I am sure you can come up with a very interesting talk. Let me know however I can contact you.
Ramanujan always the best
Ramanujan always the best
second equation is wrong x+1=sq(1+xsq(1+(x+1))sq(1+(x+2)sq(1+(x+3))))
second equation is wrong x+1=sq(1+xsq(1+(x+1))sq(1+(x+2)sq(1+(x+3))))
thank you , this is one of my try out question in my school.
quiet confused since i saw this crazy square root .lol
thank you , this is one of my try out question in my school.
quiet confused since i saw this crazy square root .lol