Equations: A Basic Introduction
Math teachers love to say "let x equal the unknown." But nobody explains why that simple trick is so powerful. Here's the thing: equations are the reason we can solve…
Math
Mathematics Blog by Gaurav Tiwari. This section is dedicated to exploring various mathematical concepts and theories, transcending the boundaries of traditional high school and early college curriculums.
The mathematics topics here encompass various subfields, including algebra, calculus, number theory, geometry, topology, and more.
Numbers – The Basic Introduction
A comprehensive guide with practical insights and actionable advice.
Mathematical Logic – The basic introduction
If mathematics is a language, then logic is its grammar. You can have brilliant mathematical intuition, but without logical precision, you can't communicate your ideas or verify they're correct. Let…
Fermat Numbers (Important Theorems & Examples)
Fermat Numbers. A comprehensive guide with practical insights and actionable advice.
Three Children, Two Friends and One Mathematical Puzzle
This is one of my favorite logic puzzles. It looks simple at first. Then you realize you're missing something. And when the solution clicks, it's genuinely satisfying. I've used this…
6 Best Social Networks for Math Majors
Handpicked and reviewed. Practical recommendations based on real testing and experience.
Vedic Multiplication: Do you multiply this way!
Before my college days, I multiplied numbers the way everyone else did - writing partial products, aligning columns, and adding everything up. It worked, but it was slow. Then I…
Russian Peasant Multiplication: The Ancient Method That Uses Only Doubling and Halving
Multiplication is probably the most important elementary operation in mathematics. Every math enthusiast develops their own preferred techniques over time. But have you ever multiplied two numbers using only doubling…
How Genius You Are?
Let have a Test: You need to make a calculation. Please do neither use a calculator nor a paper. Calculate everything "in your brain". Take 1000 and add 40. Now,…
Two Interesting Math Problems
Problem1: Smallest Autobiographical Number: A number with ten digits or less is called autobiographical if its first digit (from the left) indicates the number of zeros it contains,the second digit…
Fox-Rabbit Chase Problem [Solution & Math Proof]
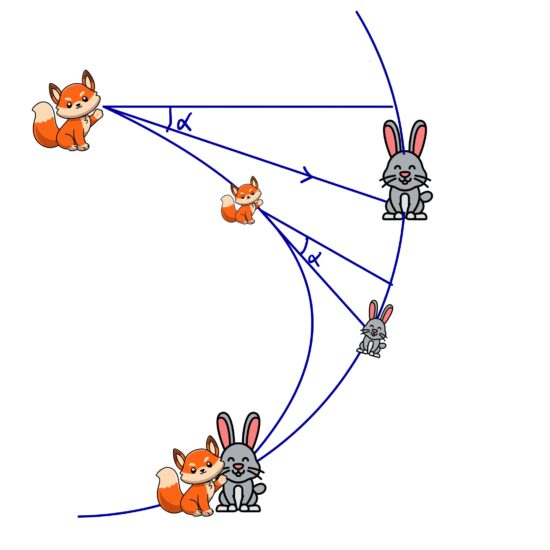
Pursuit problems are some of the most elegant challenges in classical mechanics. Two objects moving, one chasing, the other evading. The math gets surprisingly deep. This problem comes from David…
Everywhere Continuous Non-differentiable Function
Weierstrass introduced a shocking idea in 1872. There exist functions that are continuous everywhere but differentiable nowhere. Not just at a few points. At no points whatsoever. This was a…