Volume of Revolution Calculator
Use this free Volume of Revolution Calculator to compute the volume of a solid formed by rotating a region around an axis. Supports disk/washer and shell methods, multiple axes of revolution, and provides the integral formula, numerical result, and an interactive graph of the region.
Calculate the volume of a solid of revolution using disk, washer, or shell methods.
Volume
Region Visualization
Formula Used
Details
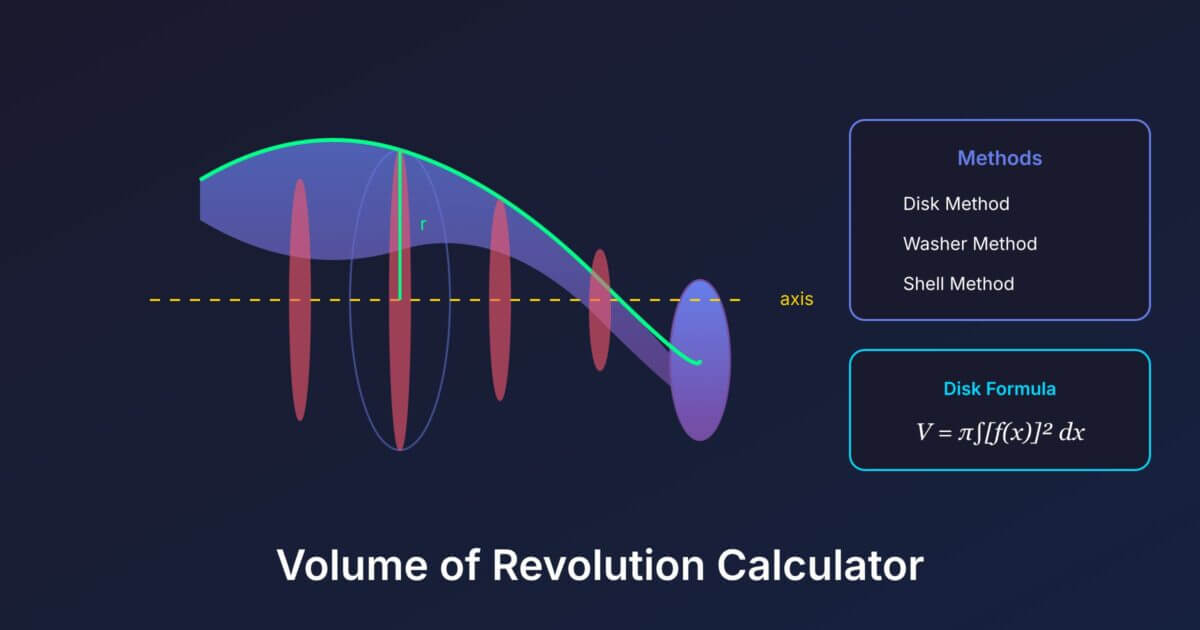
What is a Solid of Revolution?
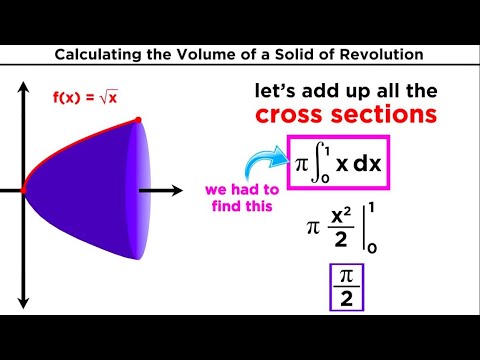
A solid of revolution is a 3D shape created by rotating a 2D region around an axis. Imagine spinning a shape around a line like a pottery wheel. The resulting solid has circular cross-sections, making it perfect for integration techniques.
Methods of Calculation
Disk Method
Used when rotating around an axis and the region touches the axis. Each cross-section is a circular disk.
$$V = \pi \int_a^b [f(x)]^2 \, dx$$
Think of stacking infinitely thin coins along the axis.
Washer Method
Used when there’s a hole in the middle (region between two curves). Each cross-section is a washer (ring).
$$V = \pi \int_a^b \left( [R(x)]^2 – [r(x)]^2 \right) dx$$
where \( R(x) \) is the outer radius and \( r(x) \) is the inner radius.
Shell Method
Uses cylindrical shells instead of disks. Often easier when rotating around the y-axis.
$$V = 2\pi \int_a^b x \cdot f(x) \, dx$$
Imagine peeling off thin cylindrical layers like an onion.
Choosing the Right Method
Use Disk/Washer When
- Rotating around a horizontal axis (x-axis or \( y = k \))
- The function is easier to express as \( y = f(x) \)
- Cross-sections perpendicular to the axis are simple
Use Shell When
- Rotating around a vertical axis (y-axis or \( x = k \))
- The function is easier to express as \( y = f(x) \)
- Solving for \( x \) would be complicated
Classic Examples
Sphere
Rotate \( y = \sqrt{r^2 – x^2} \) from \( -r \) to \( r \) around the x-axis.
$$V = \frac{4}{3}\pi r^3$$
Cone
Rotate \( y = \frac{r}{h}x \) from \( 0 \) to \( h \) around the x-axis.
$$V = \frac{1}{3}\pi r^2 h$$
Torus (Donut)
Rotate a circle around an external axis.
$$V = 2\pi^2 R r^2$$
where \( R \) is distance to axis and \( r \) is circle radius.
How to Use This Calculator
- Enter Functions – Specify the outer function \( f(x) \) and optionally an inner function \( g(x) \) for washers.
- Set Bounds – Define the x-interval for integration.
- Choose Axis – Select which axis to rotate around, or specify a custom line.
- Select Method – Pick disk/washer or shell method based on your problem.
Tips for Success
- Sketch the region before calculating
- Identify which function is “outer” and which is “inner”
- Make sure the axis of rotation doesn’t intersect the region (unless intended)
- Shell method often requires less algebra when rotating around y-axis
FAQs
When should you use disk vs shell method?
Use disk/washer when the axis of rotation is the same direction you’d naturally integrate (rotating around x-axis with y=f(x)). Use shell when they’re perpendicular (rotating around y-axis with y=f(x)). Shell avoids solving for x. For y=x², rotating around x-axis: disk is natural. Rotating around y-axis: shell avoids needing x=√y. Choose whichever makes the integral simpler.
What’s the difference between disk and washer methods?
Disk method applies when the region touches the axis of rotation, giving solid circular cross-sections. Washer method applies when there’s a gap between the region and the axis (or between two curves), giving ring-shaped cross-sections with a hole in the middle. Washer uses π(R² – r²) where R is outer radius and r is inner radius. Disk is just the special case where r = 0.
Why does the shell method use 2πr instead of πr²?
Shell method uses cylindrical shells, not disks. A thin shell at radius r with height h and thickness dr has volume ≈ 2πr·h·dr (circumference × height × thickness, like unrolling a cylinder into a rectangle). The 2πr comes from the circumference of the shell. Disk method uses πr² because you’re looking at the circular face of each disk.
How do you set up the integral for rotation around a line other than an axis?
Adjust the radius to measure distance from the rotation axis, not from the coordinate axis. For rotation around y = k, the radius becomes |f(x) – k| instead of f(x). For rotation around x = c using shells, the radius becomes |x – c|. Always draw the picture first to see whether you’re adding or subtracting from the axis position.
How is Pappus’s theorem related to volumes of revolution?
Pappus’s theorem states that the volume of a solid of revolution equals the area of the 2D region times the distance traveled by its centroid: V = 2πr̄·A, where r̄ is the centroid’s distance from the axis. For a torus made by rotating a circle of radius r around a circle of radius R, V = 2πR·(πr²) = 2π²Rr². This elegant shortcut avoids integration when you know the centroid.
What’s a common mistake when setting up volume integrals?
Subtracting functions instead of their squares. For washers, it’s π∫(R² – r²)dx, NOT π∫(R – r)²dx. Another mistake: forgetting which curve is outer vs inner, or getting the bounds wrong. Always sketch the region first. Also watch units: if rotating y = √x from 0 to 4, make sure you’re integrating with respect to x, not y (unless you’re using shells).
Can you find the volume of any 3D shape using these methods?
Only solids of revolution—shapes with circular symmetry around an axis. A sphere works (rotate semicircle). A cube doesn’t (no rotational symmetry). For non-symmetric shapes, use cross-sectional area integration: V = ∫A(x)dx where A(x) is the cross-sectional area at position x. This generalizes beyond rotation but requires knowing A(x) for each slice.
Why is the volume of a cone 1/3 the volume of a cylinder?
Using the disk method: rotate y = (r/h)x from 0 to h. The disk at position x has radius (r/h)x, so area π(rx/h)². Integrate: π(r/h)²∫x²dx from 0 to h = π(r²/h²)·(h³/3) = πr²h/3. The x² in the area formula, combined with integration, produces the 1/3 factor. A cylinder would have constant radius r, giving πr²h. The cone’s tapering radius reduces volume to exactly one-third.