Definite Integral Solver
Solve the definite integral and visualize the area under the curve.
Result
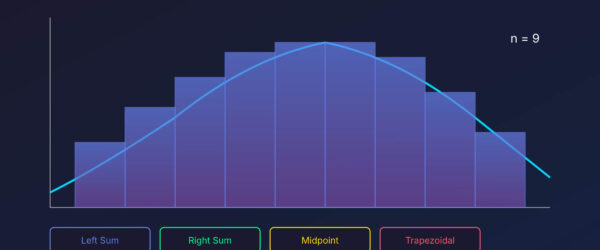
Area Visualization
Calculation Details
Use this free definite integral solver & calculator to compute exact and numerical values of integrals. Enter your function and bounds to get the result with step-by-step antiderivative computation. Perfect for calculus students and anyone needing to calculate areas under curves.
What is a Definite Integral?
A definite integral calculates the net signed area between a function and the x-axis over a specific interval. Unlike indefinite integrals which give you a family of functions, definite integrals produce a single numerical value.
The notation \( \int_a^b f(x)\,dx \) represents the integral of \( f(x) \) from \( a \) to \( b \), where \( a \) is the lower limit and \( b \) is the upper limit of integration.
The Fundamental Theorem of Calculus
If \( F(x) \) is an antiderivative of \( f(x) \), then:
$$\int_a^b f(x)\,dx = F(b) – F(a)$$
This powerful theorem connects differentiation and integration, showing they’re inverse operations.
Signed Area
Above the x-axis
When \( f(x) > 0 \), the area contribution is positive. The region between the curve and the x-axis adds to the total.
Below the x-axis
When \( f(x) < 0 \), the area contribution is negative. This is why we call it “net signed area” rather than just area.
Properties of Definite Integrals
Additivity
$$\int_a^b f(x)\,dx + \int_b^c f(x)\,dx = \int_a^c f(x)\,dx$$
You can split integrals at any point.
Reversal
$$\int_a^b f(x)\,dx = -\int_b^a f(x)\,dx$$
Swapping limits changes the sign.
Linearity
$$\int_a^b [af(x) + bg(x)]\,dx = a\int_a^b f(x)\,dx + b\int_a^b g(x)\,dx$$
Constants factor out, and integrals distribute over addition.
Applications
Physics
- Work done by a force
- Displacement from velocity
- Charge from current
- Energy calculations
Geometry
- Area between curves
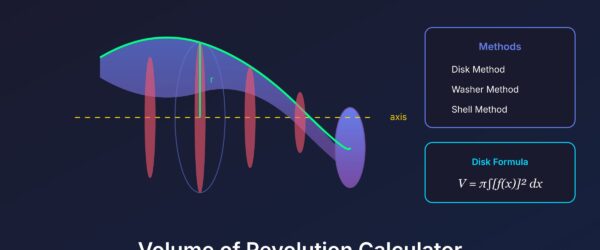
- Volume of solids
- Arc length
- Surface area
Probability
- Expected values
- Cumulative distribution functions
- Probability density integration
Common Integrals
| Function | Integral |
|---|---|
| \( x^n \) | \( \frac{x^{n+1}}{n+1} \) |
| \( \frac{1}{x} \) | \( \ln |
| \( e^x \) | \( e^x \) |
| \( \sin(x) \) | \( -\cos(x) \) |
| \( \cos(x) \) | \( \sin(x) \) |
See more Integration Formulas.
A definite integral measures signed accumulation across an interval. Area above the x-axis contributes positively and area below contributes negatively, so the result is not always the total geometric area.
How to use this calculator
Enter the integrand, lower bound, upper bound, and variable. Use parentheses around denominators and compound exponents. If the function is improper or discontinuous inside the interval, split the integral and examine each part separately.
An exact antiderivative is best when one exists. Numerical integration is the right fallback when the antiderivative is unavailable or too complicated to use.
- Check continuity and locate singularities on the interval.
- Find an antiderivative \(F\) when possible.
- Apply \(F(b)-F(a)\), keeping the lower-bound subtraction in parentheses.
- Estimate the sign and size from the graph before accepting the result.
Worked example
For \(\int_0^2(3x^2+1)\,dx\), an antiderivative is \(x^3+x\). Evaluating gives \((8+2)-(0+0)=10\).
If the question asks for total area and the function changes sign, find the zeros and split the interval. Apply an absolute value to each signed piece, not to the final combined integral.
How to read the result
Units multiply. Integrating velocity in meters per second over seconds gives displacement in meters. Integrating a rate per hour over hours gives a total amount.
Reversing the bounds changes the sign: \(\int_b^a f(x)dx=-\int_a^b f(x)dx\). Equal bounds give zero because the interval has no width.
Common mistakes to avoid
- Forgetting the constant factor from substitution.
- Subtracting the lower-bound value term by term without parentheses.
- Calling a negative integral a negative geometric area.
- Applying the Fundamental Theorem across an unhandled discontinuity.
How to verify the result
Differentiate the antiderivative returned by the solver. It should simplify to the original integrand. Then evaluate the antiderivative at both bounds and subtract lower from upper. Reversing the bounds must reverse the sign.
Compare the exact result with a rough geometric or numerical estimate. If the graph is mostly positive on an interval of width 4 and its average height is near 3, a result near 12 is reasonable; a negative or three-digit answer needs another look.
A definite integral carries the product of the integrand’s unit and the horizontal variable’s unit. It represents signed accumulation, so positive and negative regions can cancel. Use an integral of the absolute value when the problem asks for total geometric area.
Limits of the calculation
Numerical methods report approximations whose accuracy depends on smoothness, interval width, and step choice. Sharp peaks or singular behavior need special handling.
An improper integral may diverge even when a graph looks finite. Evaluate the defining limit rather than substituting the problematic endpoint.
Related calculators
Use Riemann Sum Calculator, Volume of Revolution Calculator, Arc Length Calculator when the next part of the problem needs a different method.
Useful calculus books and tools
For definite integrals, estimate the signed area from a sketch before comparing it with the exact result. Calculus answers are easier to trust when you can connect the symbolic work to a graph, an estimate, and the theorem behind the method.
- Practice beyond one example: Browse calculus textbooks and workbooks on Amazon. Look for worked problems, review exercises, and clear treatment of limits and applications.
- Sketch before calculating: Browse graph-paper notebooks on Amazon. A quick graph often reveals sign errors, incorrect bounds, and unreasonable answers.
As an Amazon Associate, I earn from qualifying purchases.
Frequently Asked Questions
What’s the difference between a definite and indefinite integral?
An indefinite integral returns a family of antiderivatives F(x) + C. A definite integral evaluates that antiderivative between two limits a and b, giving a single number: F(b) − F(a).
What does a definite integral represent geometrically?
It’s the signed area between the function’s graph and the x-axis over the interval [a, b]. Areas above the axis count positive, areas below count negative.
Does the solver handle improper integrals?
Yes — when one or both limits are infinite, or when the integrand has a singularity in the interval. It evaluates the appropriate limit and tells you whether the integral converges.
Why does my integral return ‘undefined’ or ‘divergent’?
The integral doesn’t converge. Common causes: a non-integrable singularity (like 1/x at 0), or oscillation that doesn’t settle (like sin(x) on [0, ∞)).
Can I use it for area between two curves?
Yes. Compute ∫(top − bottom) dx over the interval where they intersect. The solver returns the signed difference, so order matters.
Does it work with parametric or polar integrals?
Yes for polar (using A = ½∫r² dθ for area). For parametric area you’d compute ∫y(t)·x'(t) dt — set up the integrand explicitly.
How does the solver compute the answer?
When a closed-form antiderivative exists, it applies the Fundamental Theorem of Calculus. When it doesn’t (like ∫e^(-x²) dx), it uses adaptive numerical quadrature with controlled error tolerance.
How precise are the numerical answers?
Typically accurate to 8–10 significant figures for well-behaved integrands. Highly oscillatory or near-singular cases drop to 4–6 figures — the solver flags those when it detects them.
