Vedic Multiplication: Do you multiply this way!
Before college, I multiplied numbers the boring way. Then I discovered Vedic multiplication in a Hindi magazine called 'Bhaskar Bhoomi.' It felt like magic. I'll teach you the crisscross method…
Gaurav Tiwari is one of the top Education bloggers online, specializing in exam preparation, online learning and career development. Read these articles to prepare yourself for college and beyond. Plus, learn to earn, save and grow yourself.
Explore expert insights, study guides, and career advice tailored for students, educators, and lifelong learners. From exam preparation strategies to advanced learning techniques, this section covers everything you need to excel academically and professionally. Whether you’re preparing for competitive exams like IIT-JEE, exploring online learning platforms, or diving into subjects like math, physics, and science, you’ll find practical tips and in-depth resources here. Stay ahead with the latest trends in education, sharpen your problem-solving skills, and unlock new opportunities for growth. Let’s make learning smarter, more effective, and accessible for everyone!

Before college, I multiplied numbers the boring way. Then I discovered Vedic multiplication in a Hindi magazine called 'Bhaskar Bhoomi.' It felt like magic. I'll teach you the crisscross method…

Russian Peasant Multiplication is an ancient technique that multiplies any two numbers using only doubling and halving. No multiplication tables needed. I explain the method step by step, prove why…

Think you're good at mental math? Try this quick test. Start with 1000, add 40, add another 1000, add 30, add 1000 again, then add 20. What's your answer? Most…

Two math problems that'll make you think. First: find the smallest autobiographical number where each digit tells you how many times a digit appears. Second: a classic puzzle involving a…
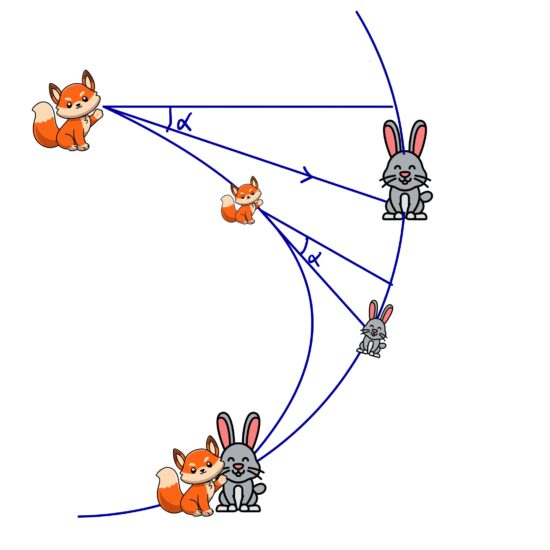
Pursuit problems are some of the most elegant challenges in classical mechanics. A fox chases a rabbit, both moving at constant speed. What path does the fox follow? I present…

Weierstrass shocked the mathematical world in 1872 by constructing a function that's continuous everywhere but differentiable nowhere. Not at a few points. At no points whatsoever. I walk through the…

Memory isn't fixed. You can train it. I've compiled ten practical methods to improve how you retain and recall information: from simple repetition and spaced practice to visualization techniques and…

I've spent years collecting free calculus textbooks. Not scanned copies with missing pages. Real textbooks that professors and universities have made freely available online. This curated list covers single-variable calculus,…

Most math students use real numbers without ever understanding how they're constructed. Dedekind solved this with his theory of cuts. He showed how to build the real numbers rigorously from…

I've compiled 20+ free algebra and topology ebooks. Not sketchy PDFs from torrent sites. Real textbooks that professors and universities have made freely available. Covers abstract algebra, linear algebra, algebraic…

The D'Alembert Ratio Test is one of the most reliable tools for determining whether an infinite series converges or diverges. I cover the theorem statement, proof, worked examples, and the…
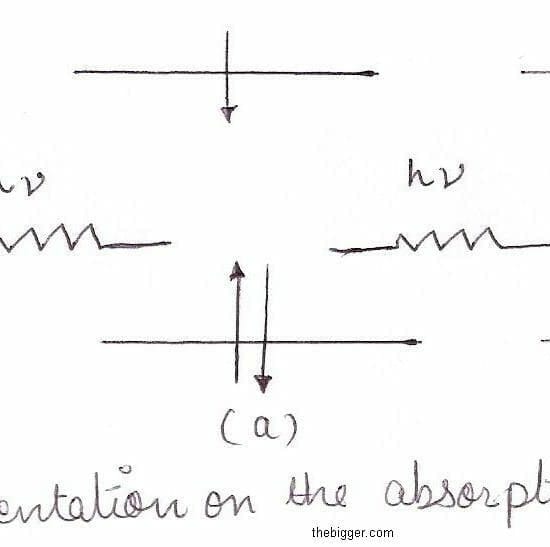
When a molecule absorbs light, the energy has to go somewhere. It can trigger a chemical reaction, release heat, or emit light as fluorescence or phosphorescence. The Jablonski diagram maps…