Vedic Multiplication: Do you multiply this way!

Before my college days, I multiplied numbers the way everyone else did – writing partial products, aligning columns, and adding everything up. It worked, but it was slow.

Then I discovered something that felt like magic.

In a Hindi magazine called “Bhaskar Lakshya,” I stumbled upon an article about multiplying numbers in a single line. No partial products. No column alignment. Just one continuous calculation from right to left.

I’ve been using this method ever since.

The Traditional Way vs. The Vedic Way

Let me show you what I mean. Say we want to multiply 187 × 54.

The traditional method looks like this:

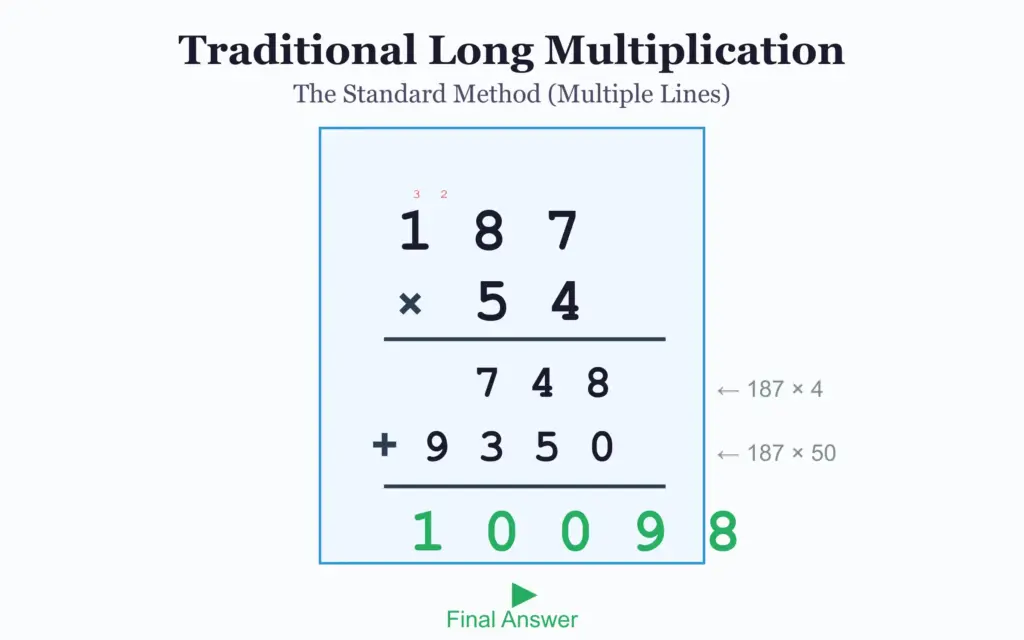
You write 187 × 4 = 748, then 187 × 5 = 935 (shifted one position), then add them together. Three separate calculations.

The Vedic method? One line. Same answer. Faster execution once you get the hang of it.

How the Vedic Method Works

This technique is called Urdhva Tiryagbhyam (ऊर्ध्व तिर्यग्भ्याम्) – Sanskrit for “vertically and crosswise.” It’s one of 16 sutras (formulas) from Vedic Mathematics, a system rediscovered by Bharati Krishna Tirtha in the early 20th century.

The core idea is simple: instead of calculating complete partial products and adding them later, you calculate each digit of the answer directly by cross-multiplying and summing as you go.

Let’s work through 498 × 753 step by step.

---

Step 1: Multiply the Units Digits

Start from the rightmost column. Multiply the units digits of both numbers.

Calculation:

• 8 × 3 = 24
• Write down 4 (the units digit)
• Carry 2 to the next step

Result so far: _ _ _ _ 4

---

Step 2: First Cross-Multiplication

Now we cross-multiply the last two digits of each number.

Calculation:

• Cross-multiply: (9 × 3) + (8 × 5) = 27 + 40 = 67
• Add the carry from Step 1: 67 + 2 = 69
• Write down 9 (the units digit of 69)
• Carry 6 to the next step

Result so far: _ _ _ 9 4

---

Step 3: The Triple Cross (Middle Position)

This is the most complex step. All three digit positions interact.

Calculation:

• Three cross-products:
• 4 × 3 = 12 (outer left to outer right)
• 9 × 5 = 45 (middle to middle)
• 8 × 7 = 56 (outer right to outer left)
• Sum: 12 + 45 + 56 = 113
• Add the carry from Step 2: 113 + 6 = 119
• Write down 9 (the units digit of 119)
• Carry 11 to the next step

Result so far: _ _ 9 9 4

---

Step 4: Second Cross-Multiplication

Mirror image of Step 2, but using the leftmost two digit pairs.

Calculation:

• Cross-multiply: (4 × 5) + (9 × 7) = 20 + 63 = 83
• Add the carry from Step 3: 83 + 11 = 94
• Write down 4 (the units digit of 94)
• Carry 9 to the next step

Result so far: _ 4 9 9 4

---

Step 5: Final Multiplication

Multiply the leftmost digits and add the final carry.

Calculation:

• Multiply: 4 × 7 = 28
• Add the carry from Step 4: 28 + 9 = 37
• Write down 37 (both digits – no more carries needed)

Final Result: 374,994

---

The Complete Pattern at a Glance

Here’s the entire process visualized:

---

When Should You Use This?

This method shines when:

1. You’re doing mental math – No paper needed once you’ve practiced
2. Speed matters – Competitive exams, quick estimates
3. You want to impress people – Seriously, multiplying 3-digit numbers in your head turns heads

The technique extends to any size numbers. Four digits? Five crosses instead of three. The pattern remains consistent.

The One Requirement

You need to be quick with basic multiplication facts and mental addition. If 8 × 7 or adding 113 + 6 requires thought, practice those first. The method amplifies your existing arithmetic speed – it doesn’t replace fundamental skills.

Try It Yourself

Here’s a practice problem:

Calculate 234 × 567

Work through the five steps:

1. Units: 4 × 7 = 28 → Write 8, carry 2
2. First cross: (3 × 7) + (4 × 6) = 21 + 24 = 45 + 2 = 47 → Write 7, carry 4
3. Triple cross: (2 × 7) + (3 × 6) + (4 × 5) = 14 + 18 + 20 = 52 + 4 = 56 → Write 6, carry 5
4. Second cross: (2 × 6) + (3 × 5) = 12 + 15 = 27 + 5 = 32 → Write 2, carry 3
5. Final: 2 × 5 = 10 + 3 = 13 → Write 13

Answer: 132,678

Check it with a calculator. Then try more problems until the pattern becomes automatic.

---

This technique transformed how I think about multiplication. It’s not just faster – it’s more elegant. You’re building the answer digit by digit, left to right across the paper, right to left in your calculation.

Once you internalize the cross-multiplication pattern, you’ll never want to go back to partial products.

Disclaimer: This site is reader‑supported. If you buy through some links, I may earn a small commission at no extra cost to you. I only recommend tools I trust and would use myself. Your support helps keep gauravtiwari.org free and focused on real-world advice. Thanks. — Gaurav Tiwari