Real Sequences: Definitions, Theorems, and Examples
Sequences are the foundation of analysis. This book provides a complete treatment from basic definitions through advanced topics like contraction mappings and fixed-point theorems. Real Sequences covers definitions, convergence criteria, important theorems, and worked examples that build deep understanding of this fundamental mathematical concept.
Sequences are the foundation of analysis. This book provides a complete treatment from basic definitions through advanced topics like contraction mappings and Picard iteration.
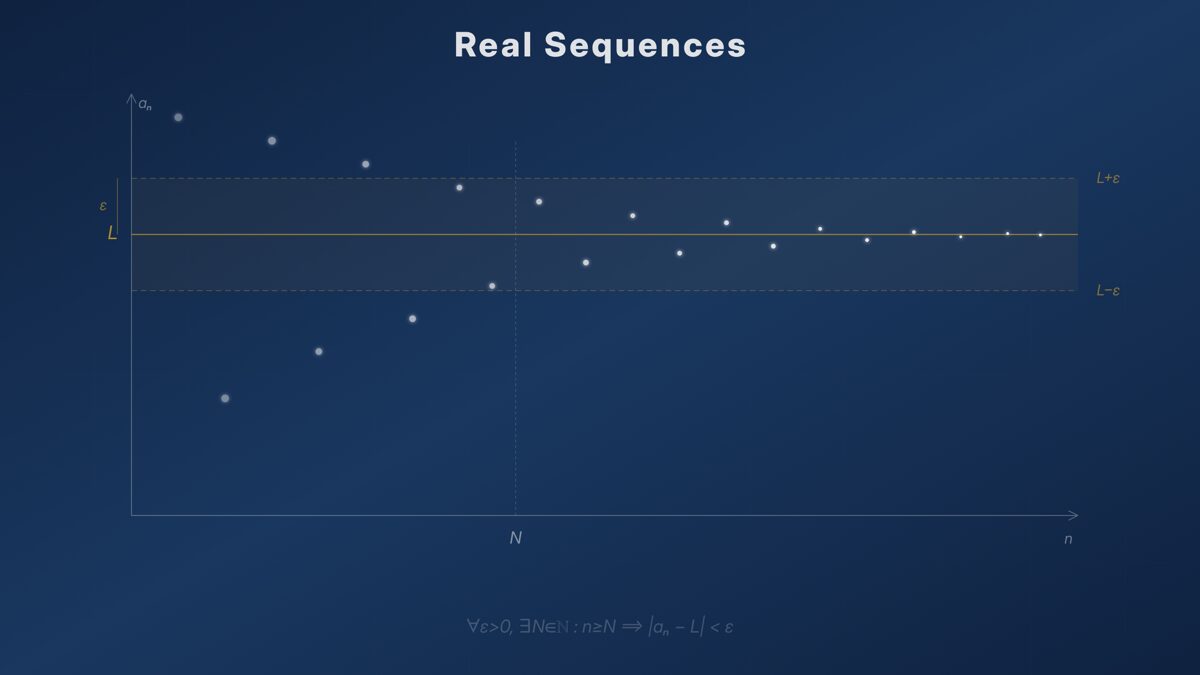
The core chapters cover convergence rigorously. The epsilon-N definition, uniqueness of limits, algebra of limits, the squeeze theorem, and convergence of subsequences.
Cauchy sequences get their own chapter, culminating in the completeness of the real numbers. The Bolzano-Weierstrass theorem is proved, and limit superior and limit inferior are defined.
The book extends to series, metric spaces, contraction mappings, and differential equations.
Topics Covered
- Epsilon-N convergence and algebra of limits
- Monotone convergence theorem and Cauchy sequences
- Bolzano-Weierstrass theorem, lim sup, and lim inf
- All standard special limits with proofs
- Series: convergence tests and key examples
- Contraction mappings, Picard iteration, and Newton’s method